From
Leetcode
Status
AC
Date
Oct 13, 2023
Tags
递归
二叉树
Difficulty
简单
题面
给你两棵二叉树:
root1 和 root2 。想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
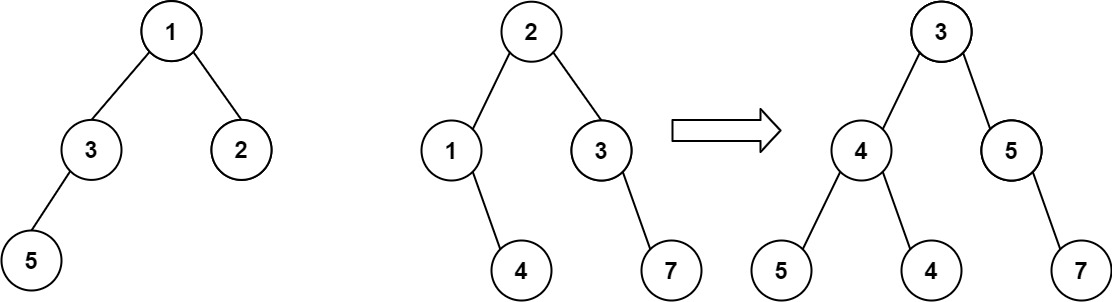
示例 2:
提示:
- 两棵树中的节点数目在范围
[0, 2000]内
104<= Node.val <= 104
思路
递归三部曲:
- 确定递归函数的参数和返回值
- 确定终止条件
- 确定单层递归的逻辑
二叉树
二叉树是一种树形结构,每个节点最多有两个子节点。以下是一些常见的二叉树类型及其特点:
- 普通二叉树:每个节点最多有两个子节点,没有其他限制。
- 完全二叉树:除了最后一层节点可以不满外,其他每层节点数都达到最大值,且最后一层的节点都靠左排列。
- 满二叉树:每个节点都有 0 或 2 个子节点,且所有叶子节点都在同一层上。
- 二叉搜索树(BST):左子树上所有节点的值都小于根节点的值,右子树上所有节点的值都大于根节点的值。
- 平衡二叉树:左右子树的高度差不超过 1,以保证树的高度不会过高。
- 红黑树:一种自平衡的二叉搜索树,通过对节点进行颜色标记和旋转操作来保持平衡。
- B树:一种多路搜索树,每个节点可以有多个子节点,用于在磁盘等外部存储设备上存储大量数据。
混乱
- 平衡二叉搜索树是不是二叉搜索树和平衡二叉树的结合?
是的,是二叉搜索树和平衡二叉树的结合。
- 平衡二叉树与完全二叉树的区别在于底层节点的位置?
是的,完全二叉树底层必须是从左到右连续的,且次底层是满的。
- 堆是完全二叉树和排序的结合,而不是平衡二叉搜索树?
堆是一棵完全二叉树,同时保证父子节点的顺序关系(有序)。 但完全二叉树一定是平衡二叉树,堆的排序是父节点大于子节点,而搜索树是父节点大于左孩子,小于右孩子,所以堆不是平衡二叉搜索树。