题面

给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。

当你在格子 (i, j) 的时候，你可以移动到以下格子之一：

• 满足 j < k <= grid[i][j] + j 的格子 (i, k) （向右移动），或者

• 满足 i < k <= grid[i][j] + i 的格子 (k, j) （向下移动）。

请你返回到达 右下角 格子 (m - 1, n - 1) 需要经过的最少移动格子数，如果无法到达右下角格子，请你返回 -1 。

示例 1：

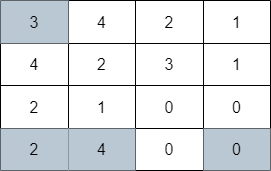
示例 2：

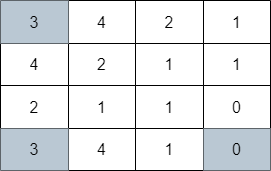
示例 3：

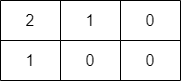
提示：

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 105

• 1 <= m * n <= 105

• 0 <= grid[i][j] < m * n

• grid[m - 1][n - 1] == 0

 

思路

1. 以行优先队列 rowQueue[i] 为例：队列中维护一个二元组 (d, j') ，其中 d 表示 dp[i][j']，用于优先队列排序；j' 为单元格的列号，结合行号 i，可以计算 grid[i][j'] + j' 来判断是否淘汰这个元素。

2. 对于当前要处理的单元格 (i, j)，首先从行优先队列 rowQueue[i] 淘汰那些无法转移到 (i, j) 的元素信息；

3. 如果最后堆为空，说明 (i, j) 左侧没有可转移到 (i, j) 的位置；否则 (i, j) 的状态就等于堆顶元素状态 d 再加 1。然后从列优先队列 colQueue[j] 中做同样处理，得到(i, j) 上侧的可转移位置并更新状态；

4. 如果两个方向都没有可转移的位置，则记 (i, j) 的状态 d = MAX （一个定义的极大值，表示不可达）。

5. 将 (i, j) 的信息分别加入所在的行优先队列和列优先队列。如果位置 (i, j) 不可达，则不加入，减少处理的状态。

题解